Planck and Rosseland Means
With the doMean option in the param.dat file, the Plank and Rosseland means,
\(\kappa_P\) and \(\kappa_R\) respectively:
and
can be calculated, where the infinity integral is truncated to the specified wavenumber limits, and \(d\nu\) is
equal to dnu set in the param.dat file.
Note that the denominators in \(\kappa_P\) and \(\kappa_R\) can be computed analytically as
and
Therefor, it is usefull to compare those analytic results to the numerical integration
and
The results of the Planck and Resseland means are stored in the file Out<name>_mean.dat, together with
the analytic and numerical expressions (10) to (13). If the numerical expressions deviate strongly
from the analytical expression, then it is a hint that the wavenumber resolution is not set fine enough.
An example of the Planck and Rosseland means is shown in Fig. 12.
doStoreFullK = 1
doMean = 1
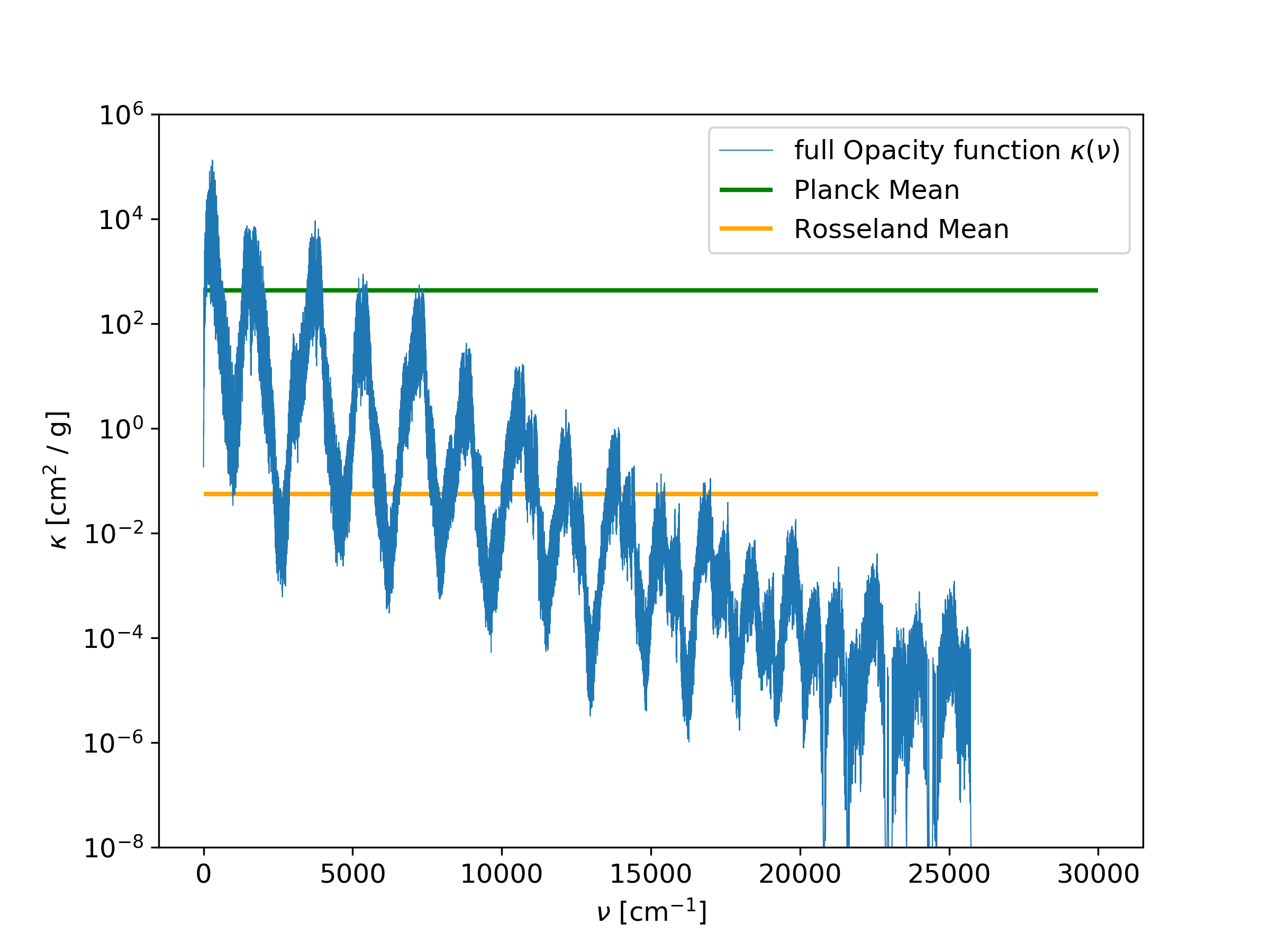
Fig. 12 Planck and Rosseland means