Resampling and k-coefficients

With the doResampling option in the param.dat file, the per bin sorted opacity function can be resampled with a Chebyshev polynomial. The number of Chebyshev can also be set in the param.dat file with the nC option. By using the resampling method, a lot of storage space can be saved. However, the exact location of individual transition lines is not contained in the resampled data. The Chebyshev coefficients are reported the Out<name>_cbin.dat files.

An example of a resampled bin is shown in Fig. 9.

Relevant parameters for this example:

  • doResampling = 1

  • nC = 20

  • doStoreSK = 2

  • nbins = 1

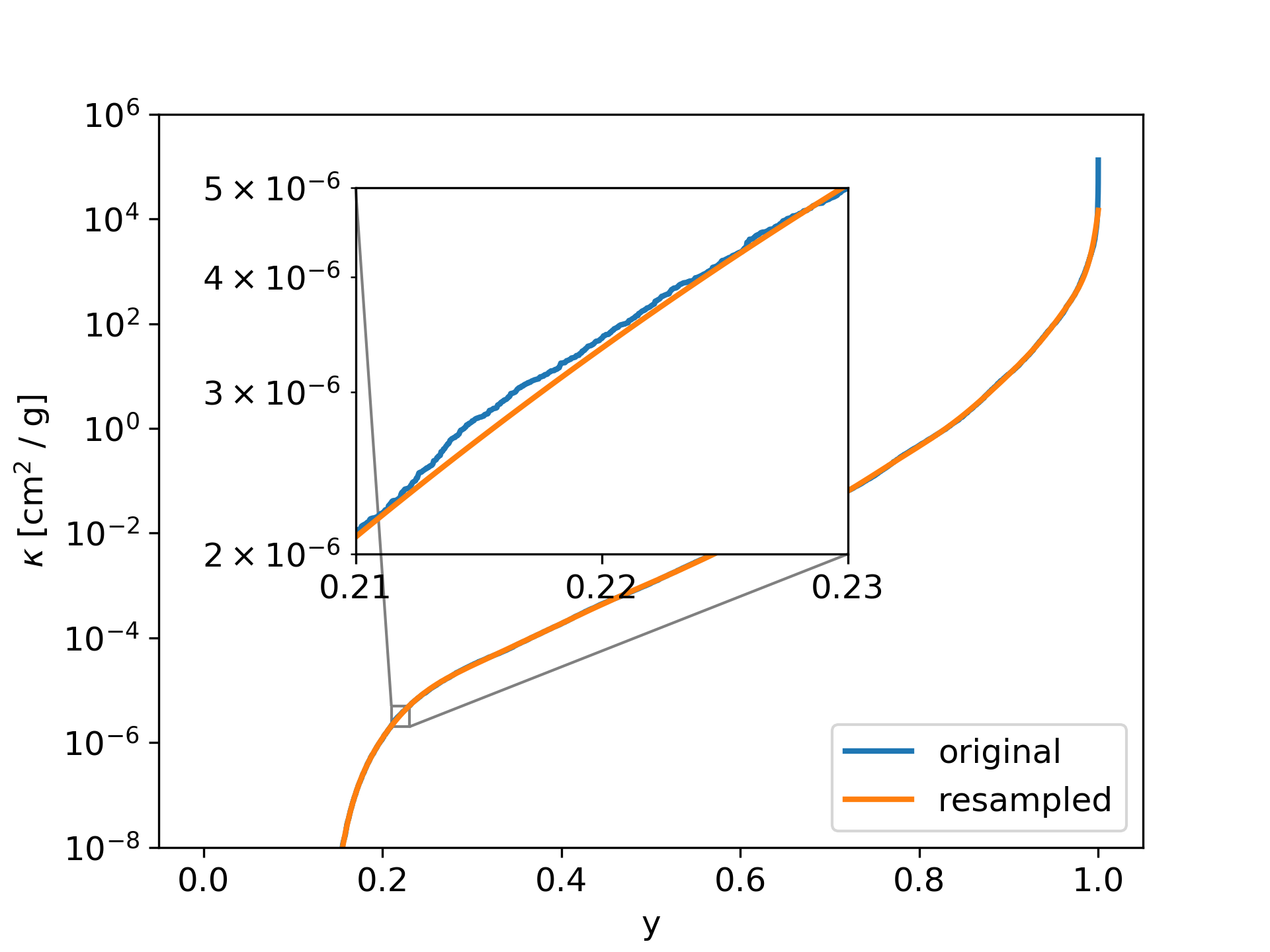
../_images/plot0017.png

Fig. 9 The per bin sorted opacity function is resampled with a Chebyshev polynomial, in order so save storage space.

Bins with empty parts

Some bins can contain an empty parts, where the opacity function have no transition lines. This empty parts causes the sorted opacity parts to have a sharp edge between the empty parts and the rest, as shown in Fig. 10. Using the Chebyshev polynomial to resample over these sharp edge would introduce oscillations into the resampled opacity functions. In order to avoid these oscillations, we resample only the part of the sorted opacity function, which is not 0 or kmin. That leads to better results, but when reconstructing the polynomial from the Chebyshev coefficients, then the empty parts must be added again. How this can be done is shown next.

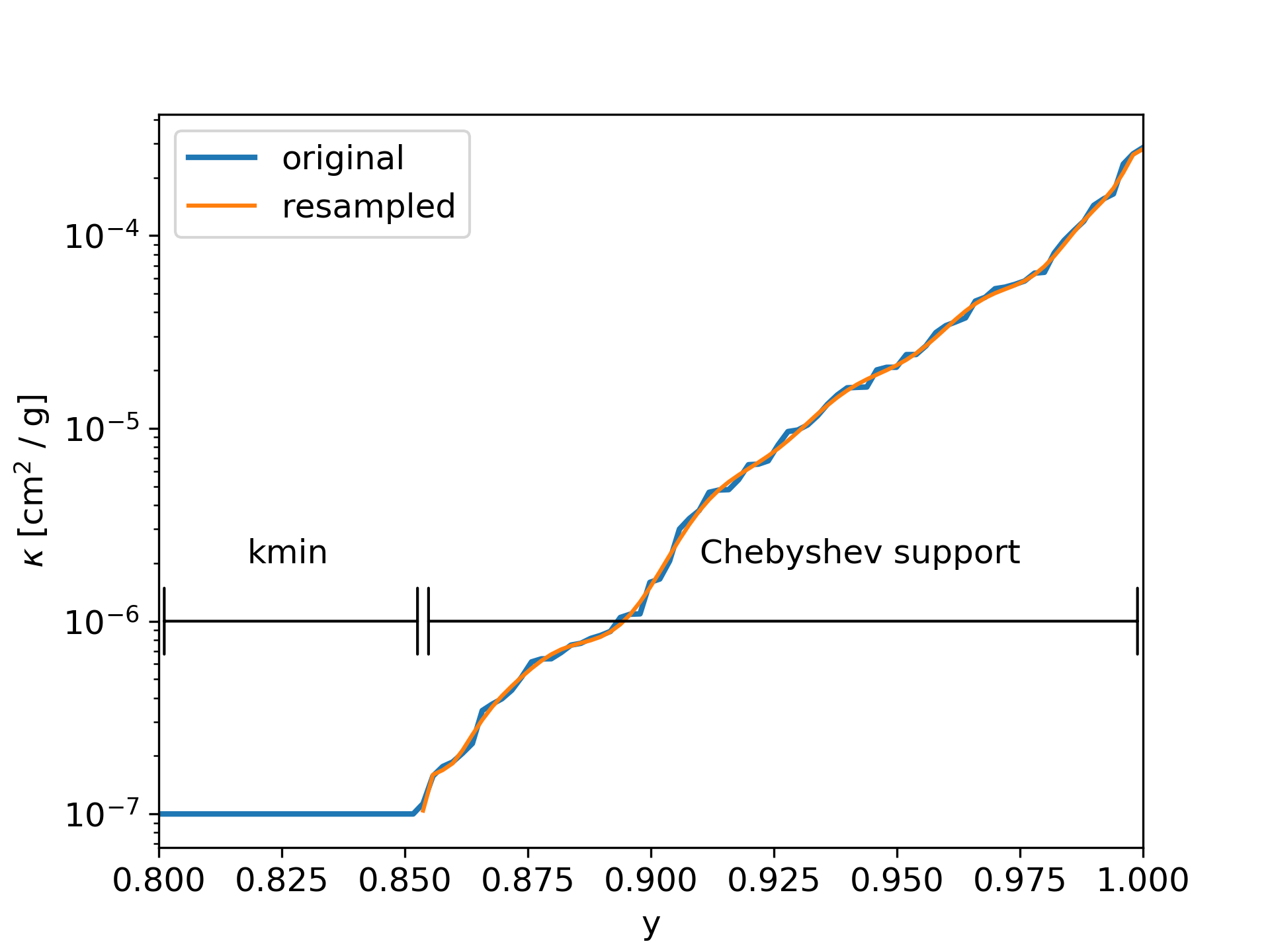
../_images/plot0018.png

Fig. 10 Resampling a bin with an empty part. To avoid oscillations in the resampled Polynoial, only values > kmin are considered.

Using the Chebyshev coefficients

The resampled opacity function can be reconstruced with the following code: (See also the code recon_bin.py in the tools directory)

import numpy as np
from numpy.polynomial.chebyshev import chebval

#change here the name of the file
data_c = np.loadtxt('Out_name_cbin.dat')

#change here the bin index and the bin size:
binIndex = 0
binSize = 300

x = np.linspace(0, 1.0, num=binSize, endpoint=True)

#extract Chebyshev coefficients
c = data_c[binIndex,2:]
#extract starting point in x of opacity function
xs = data_c[binIndex,1]

#rescale x to the standard Chebychev polynomial range [-1:1]
x1 = x * 2.0 - 1.0
k_res = chebval(x1,c,tensor=False)
x2 = x * (1.0 - xs) + xs

#result is in k_res for x values in x2
k_res = np.exp(k_res)