Line Profiles
HELIOS-K supports four different line profiles which can be set by the
profile parameter.The supported profiles are:
1: Voigt
2: Lorentz
(1)\[f_L(\nu) = \frac{1}{\pi} \frac{\gamma_L}{(\nu - \nu_0)^2 + \gamma_L^2}\]
3: Doppler
(2)\[f_G(\nu) = \sqrt{\frac{ln(2)}{\pi}} \frac{1}{\alpha_D} \exp\left(-\frac{ (\nu - \nu_0)^2 ln(2)}{\alpha_D^2} \right)\]
4: Binned Gaussian integrated cross section
(3)\[f_{BG} = \frac{1}{\Delta \nu} \int_{\nu - \nu/2}^{\nu + \nu/2} f_G(\nu) d \nu = \frac{1}{2 \Delta \nu} \left[ erf(\chi^+) - erf(\chi^-) \right]\]
[Yurchenko et al. 2018: (ExoCross : a general program for generating spectra from molecular line lists)]
with the Doppler half-width:
(4)\[\alpha_D = \frac{\nu}{c} \sqrt{\frac{2 ln(2) k_B T}{m}}\]
and the Lorentz half-width for Hitran like data:
(5)\[\gamma_L = \frac{A}{4\pi c} + \left( \frac{T}{T_{ref}}\right)^{-n} \left[ \frac{\alpha_{air} (P-P_{self})}{P_{ref}} + \frac{\alpha_{self} P_{self}}{P_{ref}}\right]\]
or the Lorentz half-width for ExoMol like data:
(6)\[\gamma_L = \frac{A}{4\pi c} + \left( \frac{T_{ref}}{T} \right)^n \cdot \left( \frac{P}{P_{ref}}\right)\]
or the Lorentz half-width for Atomic data:
(7)\[\gamma_L = \frac{\Gamma_{nat}}{4\pi c} + \left( \frac{T_{ref}}{T} \right)^n \cdot \left( \frac{P}{P_{ref}}\right)\]
In Fig. 2 is shown an example with four different line profiles.
Relevant parameters for this example:
doStoreFullK = 1
profile = 1 or 2 or 3 or 4
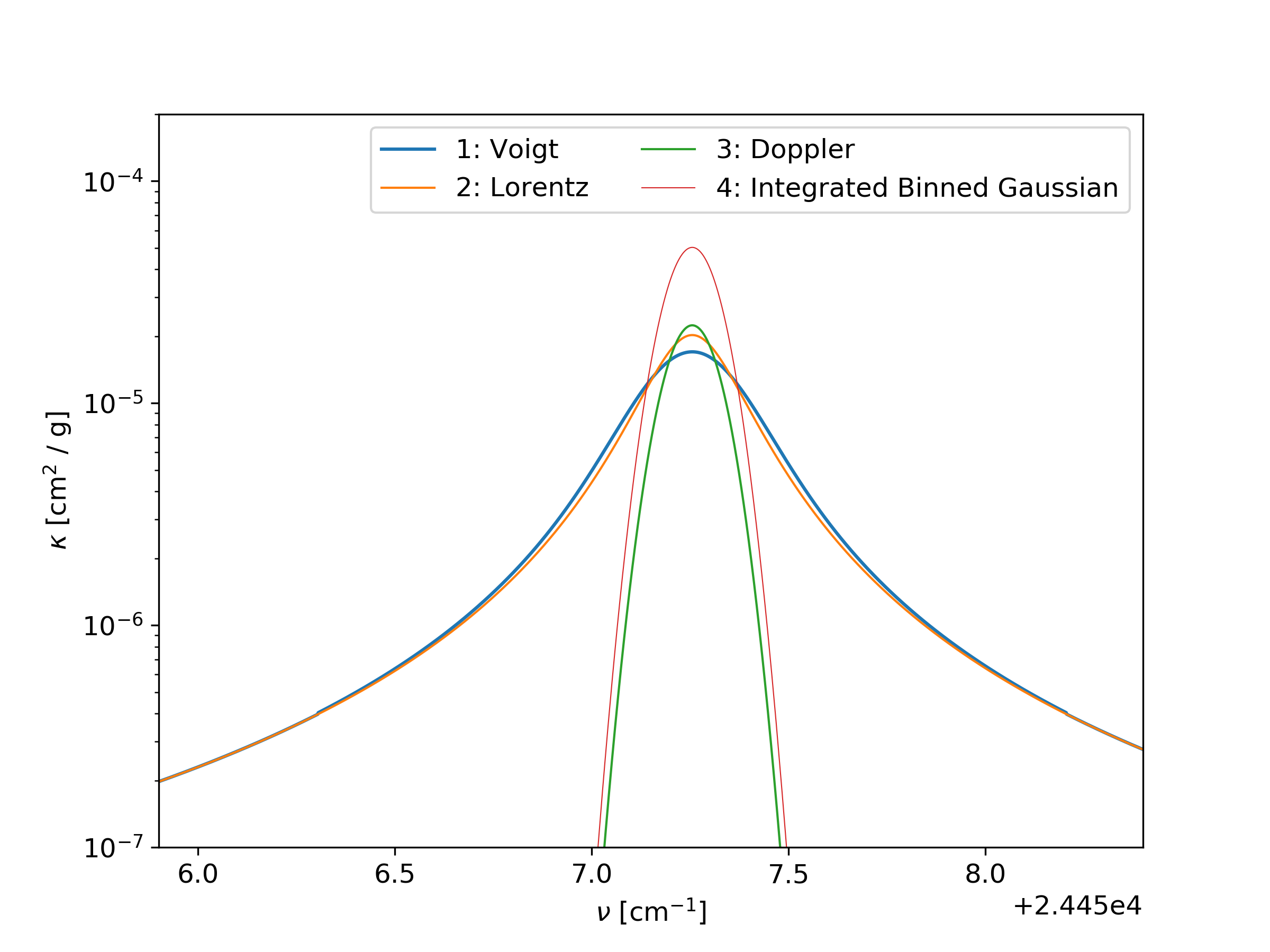
Fig. 2 Example with four different line profiles